I think I have the proof.
The problem is, that the Kapex manual made some simplistic assumptions. Technically speaking, the formula is not correct. I will have to draw pictures tomorrow, but here is what I have.
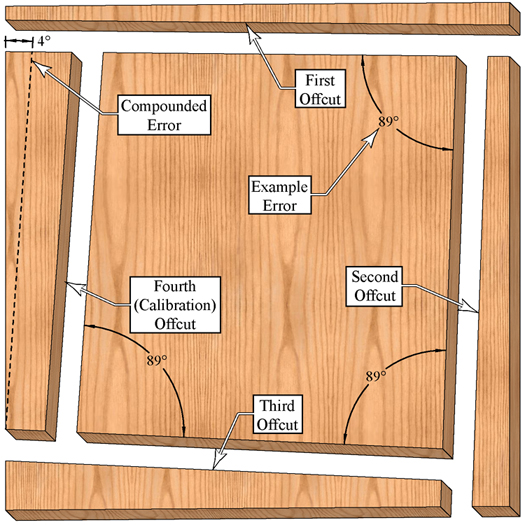
The final offcut is a trapezoid like figure (but not a trapezoid!). For simplicity's sake, let's use Kapex's example of each cut being off 1 degree. Also, assume the final length is 500 mm. If you start on the upper left and move clockwise, you get angles of 91, 93, 89, and 87. You have no right triangles, and no equal sides. Strictly speaking, you can't use trigonometry to solve the problem at all.
But if you make some simplistic assumptions, you can. First, we can make two right triangles form the trapezoid like figure. On triangle will angles of 1, 89, and 90 degrees. The second one will have angles measuring 3, 87, and 90 degrees. The sum of the bases of the triangles will give the error. But we have to make some assumptions.
Assumptions 1: assume the hypotenuse of each triangle is equal. In our example one hypotenuse was .6 mm different. That is a small amount, especially considering it is unlikely you will have a measure off by a full degree.
Assumption 2: assume sin(e) + sin(3e) = sin(4e), where e is the error of the cut, in our case 1 degree. Strictly speaking, this math is wrong, and you can't do this. But for small angles, it will work out okay.
So the real formula is: [WidthLeft - WidthRight/Length] = sin(e) + sin(3e)
If you assume sin(e) + sin(3e) = sin(4e) you can solve for e:
[WidthLeft - WidthRight/Length] = sin(4e)
arcsin[widthLeft - WidthRight/Length] = 4e
1/4 arcsin[widthLeft - WidthRight/Length] = e
Two disclaimers here. First, I could have easily made a mistake. If so, I am open to corrections. I only posted this because I have worked and re-worked the problem, and I believe I have it right.
Second, I am not implying in any way that the Kapex manual made a blunder. It is a perfectly acceptable strategy to make the simplistic assumptions the manual made in order to solve a real world problem. I am thinking back to calculus when I had to differentiate a problem that would not solvable, until you realized the number e became insignificant as you approached a limit. The course was pure math, and if that strategy was applicable there, it is certainly applicable here.
This was a tough problem because, given Kapex's formula, I assumed there was a simple solution, or at least one that didn't involve bending some rules.
To be clear, my document as it stands is in error. You should not add up the sides. The final piece gives you all the dimensions you need. I will update my document tomorrow and include a section at the end explaining the math. I couldn't find any real math explanations on the web.