- Joined
- Jan 22, 2007
- Messages
- 1,641
paulhtremblay said:The problem is, that the Kapex manual made some simplistic assumptions.
Given the length of your posting, I assume you started writing this before I made my posting above. You need to go back and look at that, because you are approaching your proof incorrectly, and assume that I did the same.
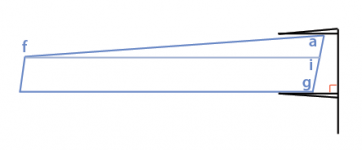
No, the Kapex manual did not make any assumptions or simplifications in any way. It actually assumes the worst, such as the example graphic below.
The image below is a remake of the Kapex image, except is starts out with an exaggerated non-square polygon. You can clearly see why you cannot base your proof on using the offcut pieces until you reach the 4th offcut. Even though I added the annotations in Adobe Illustrator, this is a SolidWorks model and is not an approximation and it is fully dimensioned back in SolidWorks.
Edit: I've updated the image below to add the RED 89 degree angle that I didn't have room to show back in the Kapex manual. Sorry it's so blurry.
[attachimg=1]